【理論】令和5年(上期) 問9|交流R-L直列回路における力率の求め方に関する計算問題
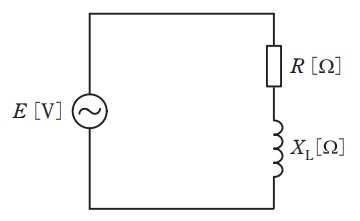
図のように,抵抗 \( R \) [Ω] と誘導性リアクタンス \( X_L \) [Ω] が直列に接続された交流回路がある。
\( \displaystyle \frac {R}{X_{\mathrm {L}}}=\frac {1}{\sqrt {2}} \) の関係があるとき,この回路の力率 \( \cos \phi \) の値として,最も近いものを次の \( (1) \) ~ \( (5) \) のうちから一つ選べ。
合格への方程式
交流回路とインピーダンス
交流回路では、抵抗・コイル・コンデンサなどの素子における電圧と電流の関係を表すために「インピーダンス」という概念を用います。
インピーダンスとは:
交流回路における電圧と電流の比を表す複素数の量です。単位はオーム [Ω] です。
\[ \begin{eqnarray} \dot{Z} &=& \frac{\dot{V}}{\dot{I}} \end{eqnarray} \]
ここで、ドット(˙)は複素数を表します。
基本素子のインピーダンス:
抵抗 R [Ω]、コイル L [H]、コンデンサ C [F] のインピーダンスは、角周波数 ω [rad/s] を用いて次のように表されます:
\[ \begin{eqnarray} \dot{Z}_{\mathrm{R}} &=& R \\[10pt] \dot{Z}_{\mathrm{L}} &=& \mathrm{j}\omega L &=& \mathrm{j}2\pi f L \\[10pt] \dot{Z}_{\mathrm{C}} &=& \frac{1}{\mathrm{j}\omega C} &=& \frac{1}{\mathrm{j}2\pi f C} \end{eqnarray} \]
j の意味:
j は虚数単位(j² = -1)を表し、位相の違いを表現するために使用されます。電気工学では、数学の i の代わりに j を使用するのが一般的です。
インピーダンスの直列接続と並列接続:
抵抗と同様に、インピーダンスも直列・並列の接続規則があります:
- 直列接続: Z = Z₁ + Z₂ + Z₃ + ...
- 並列接続: 1/Z = 1/Z₁ + 1/Z₂ + 1/Z₃ + ...
インピーダンスの複素表現:
インピーダンスは一般的に次のように表されます:
\[ \begin{eqnarray} \dot{Z} &=& R + \mathrm{j}X \end{eqnarray} \]
ここで:
- R:抵抗成分(実部)
- X:リアクタンス成分(虚部)
リアクタンス X は、コイルの場合は正(誘導性リアクタンス XL = ωL)、コンデンサの場合は負(容量性リアクタンス XC = -1/ωC)となります。
R・L・C素子の電圧と電流の関係
交流回路の各素子では、電圧と電流の間に特徴的な位相関係があります。
抵抗 R の場合:
\[ \begin{eqnarray} \dot{V}_{\mathrm{R}} &=& R\dot{I} \end{eqnarray} \]
抵抗では、電圧と電流は同相(位相差なし)です。
コイル L の場合:
\[ \begin{eqnarray} \dot{V}_{\mathrm{L}} &=& \mathrm{j}\omega L \dot{I} \end{eqnarray} \]
コイルでは、電圧は電流よりも位相が90°進みます。
コンデンサ C の場合:
\[ \begin{eqnarray} \dot{V}_{\mathrm{C}} &=& \frac{\dot{I}}{\mathrm{j}\omega C} \end{eqnarray} \]
コンデンサでは、電圧は電流よりも位相が90°遅れます。
ベクトル図での表現:
これらの位相関係は、ベクトル図を用いて視覚的に表現できます。電流ベクトルを基準(横軸)として:
- 抵抗の電圧ベクトル: 電流と同じ方向(0°)
- コイルの電圧ベクトル: 電流より90°進んだ方向(上向き)
- コンデンサの電圧ベクトル: 電流より90°遅れた方向(下向き)
覚え方のヒント:
「ELI the ICE man」という覚え方があります。
- ELI: E(電圧)は L(コイル)の I(電流)より前に来る → 電圧が電流より進む
- ICE: I(電流)は C(コンデンサ)の E(電圧)より前に来る → 電流が電圧より進む
周波数依存性:
コイルとコンデンサのインピーダンスは周波数に依存します:
- コイル:周波数が高いほどインピーダンスが大きくなる
- コンデンサ:周波数が高いほどインピーダンスが小さくなる
交流回路における電力の種類
交流回路では、電力には複数の種類があります。それぞれが回路内のエネルギーの異なる側面を表しています。
1. 有効電力 P [W]:
実際に熱や仕事などの形で消費される電力です。抵抗成分のみが有効電力を消費します。
\[ \begin{eqnarray} P &=& RI^2 \end{eqnarray} \]
2. 無効電力 Q [var]:
リアクタンス成分(コイルやコンデンサ)での電力のやり取りを表します。エネルギーが電源と素子間を行き来するだけで、実際には消費されません。
\[ \begin{eqnarray} Q &=& XI^2 \end{eqnarray} \]
X はリアクタンスで、コイルでは正(XL = ωL)、コンデンサでは負(XC = -1/ωC)となります。
3. 皮相電力 S [VA]:
有効電力と無効電力のベクトル和で、実際に電源から供給される見かけの電力です。
\[ \begin{eqnarray} S &=& \sqrt{P^2 + Q^2} \\[10pt] &=& ZI^2 \end{eqnarray} \]
Z はインピーダンスの絶対値(大きさ)です。
電力の単位:
- 有効電力 P:ワット [W]
- 無効電力 Q:バール [var](volt-ampere reactive)
- 皮相電力 S:ボルトアンペア [VA]
異なる単位を使用することで、電力の種類を区別しやすくしています。
各素子での電力:
- 抵抗 R:有効電力のみを消費(P = RI²、Q = 0)
- 理想コイル L:無効電力のみを消費(P = 0、Q = ωLI²)
- 理想コンデンサ C:無効電力のみを消費(P = 0、Q = -I²/ωC)
力率と電力三角形
力率(パワーファクター)は、交流回路における電力の効率を表す重要な指標です。
力率の定義:
力率は有効電力と皮相電力の比で、cosθ で表されます:
\[ \begin{eqnarray} \cos\theta &=& \frac{P}{S} \\[10pt] &=& \frac{R}{Z} \\[10pt] &=& \frac{R}{\sqrt{R^2 + X^2}} \end{eqnarray} \]
ここで θ は、電圧と電流の位相差(インピーダンス角)です。
電力三角形:
有効電力 P、無効電力 Q、皮相電力 S の関係は、直角三角形(電力三角形)として表現できます:
- 底辺:有効電力 P [W]
- 高さ:無効電力 Q [var]
- 斜辺:皮相電力 S [VA]
- 底辺と斜辺のなす角:位相角 θ
力率の特徴:
- 力率の範囲:0 ≤ cosθ ≤ 1
- 力率 = 1(cosθ = 1):理想的な状態、有効電力のみで無効電力はゼロ
- 力率 = 0(cosθ = 0):最悪の状態、無効電力のみで有効電力はゼロ
力率の種類:
- 遅れ力率: インダクタンス(コイル)が支配的な回路(電流が電圧より遅れる)
- 進み力率: キャパシタンス(コンデンサ)が支配的な回路(電流が電圧より進む)
力率改善の重要性:
低い力率は以下の問題を引き起こします:
- 電力損失の増加(送電線での熱損失)
- 電気設備の容量不足(同じ有効電力に対して大きな皮相電力が必要)
- 電圧降下の増加
これらの問題を解決するため、産業用の大型機器ではコンデンサバンクを設置して力率を改善(力率改善用コンデンサ)することが一般的です。
インピーダンス三角形:
電力三角形と同様に、インピーダンスの関係も三角形で表現できます:
- 底辺:抵抗 R [Ω]
- 高さ:リアクタンス X [Ω]
- 斜辺:インピーダンスの大きさ Z [Ω]
- 底辺と斜辺のなす角:位相角 θ
これにより、インピーダンスと電力の三角形は相似となります。
計算問題
インピーダンスと電力に関する計算問題を解いてみましょう。
問題1:RLC直列回路のインピーダンス
抵抗 R = 100 Ω、コイル L = 0.2 H、コンデンサ C = 20 μF が直列に接続された回路があります。この回路の周波数 f = 50 Hz におけるインピーダンスと位相角を求めなさい。
解答:
まず、各素子のリアクタンスを計算します。
\[ \begin{eqnarray} X_L &=& 2\pi f L \\[10pt] &=& 2\pi \times 50 \text{ Hz} \times 0.2 \text{ H} \\[10pt] &\approx& 62.8 \text{ Ω} \end{eqnarray} \]
\[ \begin{eqnarray} X_C &=& \frac{1}{2\pi f C} \\[10pt] &=& \frac{1}{2\pi \times 50 \text{ Hz} \times 20 \times 10^{-6} \text{ F}} \\[10pt] &\approx& 159.2 \text{ Ω} \end{eqnarray} \]
合成リアクタンスは:
\[ \begin{eqnarray} X &=& X_L - X_C \\[10pt] &=& 62.8 \text{ Ω} - 159.2 \text{ Ω} \\[10pt] &=& -96.4 \text{ Ω} \end{eqnarray} \]
インピーダンスの大きさは:
\[ \begin{eqnarray} Z &=& \sqrt{R^2 + X^2} \\[10pt] &=& \sqrt{(100 \text{ Ω})^2 + (-96.4 \text{ Ω})^2} \\[10pt] &=& \sqrt{10000 + 9293} \\[10pt] &\approx& 138.9 \text{ Ω} \end{eqnarray} \]
位相角は:
\[ \begin{eqnarray} \theta &=& \tan^{-1}\left(\frac{X}{R}\right) \\[10pt] &=& \tan^{-1}\left(\frac{-96.4}{100}\right) \\[10pt] &\approx& -43.9 \text{ 度} \end{eqnarray} \]
位相角が負であるため、この回路は容量性(コンデンサが支配的)であり、電流が電圧より進むことを示しています。
問題2:電力の計算
インピーダンス Z = 50 + j30 Ω の回路に電流 I = 2 A が流れています。この回路の有効電力、無効電力、皮相電力および力率を求めなさい。
解答:
まず、各パラメータを確認します:
- 抵抗成分 R = 50 Ω
- リアクタンス成分 X = 30 Ω
- 電流 I = 2 A
有効電力は:
\[ \begin{eqnarray} P &=& RI^2 \\[10pt] &=& 50 \text{ Ω} \times (2 \text{ A})^2 \\[10pt] &=& 200 \text{ W} \end{eqnarray} \]
無効電力は:
\[ \begin{eqnarray} Q &=& XI^2 \\[10pt] &=& 30 \text{ Ω} \times (2 \text{ A})^2 \\[10pt] &=& 120 \text{ var} \end{eqnarray} \]
皮相電力は:
\[ \begin{eqnarray} S &=& \sqrt{P^2 + Q^2} \\[10pt] &=& \sqrt{(200 \text{ W})^2 + (120 \text{ var})^2} \\[10pt] &=& \sqrt{40000 + 14400} \\[10pt] &=& \sqrt{54400} \\[10pt] &\approx& 233.2 \text{ VA} \end{eqnarray} \]
または、インピーダンスの大きさから:
\[ \begin{eqnarray} Z &=& \sqrt{R^2 + X^2} \\[10pt] &=& \sqrt{(50 \text{ Ω})^2 + (30 \text{ Ω})^2} \\[10pt] &=& \sqrt{2500 + 900} \\[10pt] &=& 58.3 \text{ Ω} \end{eqnarray} \]
\[ \begin{eqnarray} S &=& ZI^2 \\[10pt] &=& 58.3 \text{ Ω} \times (2 \text{ A})^2 \\[10pt] &=& 233.2 \text{ VA} \end{eqnarray} \]
力率は:
\[ \begin{eqnarray} \cos\theta &=& \frac{P}{S} \\[10pt] &=& \frac{200 \text{ W}}{233.2 \text{ VA}} \\[10pt] &\approx& 0.857 \end{eqnarray} \]
または:
\[ \begin{eqnarray} \cos\theta &=& \frac{R}{Z} \\[10pt] &=& \frac{50 \text{ Ω}}{58.3 \text{ Ω}} \\[10pt] &\approx& 0.857 \end{eqnarray} \]
リアクタンスが正(誘導性)であるため、この回路は遅れ力率であり、電流が電圧より遅れています。
🔍 ワンポイントアドバイス: インピーダンスと電力の関係を理解するときは、三角形(インピーダンス三角形と電力三角形)を視覚的にイメージすると理解しやすくなります。両者は相似形であり、抵抗 R と有効電力 P、リアクタンス X と無効電力 Q、インピーダンス Z と皮相電力 S がそれぞれ対応しています。また、複素数計算が苦手な場合は、ベクトル図を描いて各素子の電圧・電流の位相関係を確認すると良いでしょう。特に「ELI the ICE man」の語呂合わせを覚えておくと、コイルとコンデンサの位相関係を間違えにくくなります。
今日は交流回路の力率について勉強していくで!力率は電気設備の効率を考える上でめっちゃ重要やからな。
まず力率ってなんやろうか?簡単に説明してみ?
はい、先生!力率とは、交流回路において、見かけの電力(皮相電力)に対する有効電力の比率のことです。数式では cos φ と表され、0から1の間の値をとります。φは電圧と電流の位相差です。
力率が高いほど(1に近いほど)、電力の利用効率が良いことを意味します。一方、力率が低いと、同じ仕事をするのにより多くの電流が必要になり、電線の損失が増えたり、設備容量を大きくする必要が出てきます。
ええやん!力率の基本をしっかり理解できてるな。力率は cos φ で表されて、これは電圧と電流の位相差のコサインやね。
さて、実際の計算に入っていこか。力率の計算方法はいくつかあるんやけど、抵抗 R とリアクタンス X を使った計算方法を知ってるか?
はい、先生!抵抗RとリアクタンスXを使った力率の計算方法は以下の通りです:
\[ \cos \phi = \frac{R}{Z} = \frac{R}{\sqrt{R^2 + X^2}} \]ここで:
- R は抵抗 [Ω]
- X はリアクタンス [Ω](誘導性の場合はXL、容量性の場合はXC)
- Z はインピーダンス [Ω]
この式は、インピーダンス三角形から導かれるもので、力率は抵抗Rをインピーダンスの大きさZで割ったものになります。
さすがやな!力率の計算式をしっかり理解してるね。今回は具体的な問題を解いていこか。
ある回路で抵抗Rと誘導性リアクタンスXLがあるとする。ここでXL = √2・Rの関係があるとき、この回路の力率cos φはいくらになるやろうか?計算してみてや。
はい、先生!計算してみます。
与えられた条件は:
\(X_L = \sqrt{2} \cdot R\)
力率の計算式に代入します:
\[ \begin{aligned} \cos \phi &= \frac{R}{\sqrt{R^2 + X_L^2}} \\ &= \frac{R}{\sqrt{R^2 + (\sqrt{2} \cdot R)^2}} \\ &= \frac{R}{\sqrt{R^2 + 2R^2}} \\ &= \frac{R}{\sqrt{3R^2}} \\ &= \frac{R}{\sqrt{3} \cdot R} \\ &= \frac{1}{\sqrt{3}} \\ &\approx 0.58 \end{aligned} \]したがって、この回路の力率は約0.58、つまり58%となります。
完璧や!計算が正確で、力率が1/√3 ≒ 0.58になることをちゃんと導き出せたな。
さて、この力率0.58というのは良い値やと思うか?実用上はどうなんやろう?
いいえ、先生。力率0.58という値は実用上あまり良い値とは言えません。
一般的に、電力会社は需要家(電気の使用者)に対して力率を0.85以上、理想的には0.95以上に保つことを求めています。力率が低いと以下のような問題が生じます:
- 同じ有効電力を供給するのにより大きな電流が必要になり、送電線やケーブルの損失が増加します
- 変圧器や発電機など、電力設備の容量をより大きくする必要があります
- 電圧降下が大きくなり、電圧変動の原因になります
- 多くの電力会社は、力率が低い大口需要家に対して割増料金を課しています
このような理由から、力率0.58の回路は改善が必要で、通常は力率改善用のコンデンサを設置して力率を向上させます。
ほんまによう理解してるな!力率0.58は低すぎて、実際の設備ではあかんね。電力会社は通常、85%以上の力率を求めてるんや。
今の回路は誘導性負荷で遅れ力率やけど、これを改善するにはどうしたらええか知ってるか?
はい、先生!誘導性負荷(遅れ力率)の力率を改善するには、回路に並列にコンデンサを接続します。
コンデンサは容量性リアクタンスXCを持ち、誘導性リアクタンスXLと逆の特性を示します。コンデンサを適切な容量で接続することで、回路全体の無効電力成分を減少させ、力率を改善することができます。
この方法を「力率改善」または「力率補償」と呼びます。実際には、コンデンサバンクという形で設置されることが多く、負荷の変動に応じて段階的に容量を切り替えられるようになっています。
適切なコンデンサ容量は、目標とする力率と現在の力率から計算することができます。
その通りや!力率改善には並列にコンデンサをつなぐんやね。じゃあ具体的に、今の回路(力率0.58)を力率0.9まで改善するには、どれくらいの容量のコンデンサが必要か計算してみよか?
有効電力Pが1000W、電源電圧が100Vとして計算してみてや。
はい、先生!計算してみます。
まず、現在の状態と改善後の状態を整理します:
- 現在の力率:cos φ1 = 0.58(遅れ)
- 目標の力率:cos φ2 = 0.9(遅れ)
- 有効電力:P = 1000 W
- 電源電圧:V = 100 V
力率から位相角を求めます:
\(\phi_1 = \cos^{-1}(0.58) \approx 54.7^{\circ}\)
\(\phi_2 = \cos^{-1}(0.9) \approx 25.8^{\circ}\)
現在の皮相電力S1と無効電力Q1を求めます:
\[ \begin{aligned} S_1 &= \frac{P}{\cos \phi_1} = \frac{1000}{0.58} \approx 1724 \ \mathrm{[VA]} \\ Q_1 &= S_1 \sin \phi_1 = 1724 \sin(54.7^{\circ}) \approx 1410 \ \mathrm{[var]} \end{aligned} \]改善後の皮相電力S2と無効電力Q2を求めます:
\[ \begin{aligned} S_2 &= \frac{P}{\cos \phi_2} = \frac{1000}{0.9} \approx 1111 \ \mathrm{[VA]} \\ Q_2 &= S_2 \sin \phi_2 = 1111 \sin(25.8^{\circ}) \approx 484 \ \mathrm{[var]} \end{aligned} \]必要なコンデンサの無効電力QCは、現在の無効電力Q1と改善後の無効電力Q2の差です:
\[ \begin{aligned} Q_C &= Q_1 - Q_2 \\ &= 1410 - 484 \\ &= 926 \ \mathrm{[var]} \end{aligned} \]コンデンサの容量Cは以下の式で計算できます:
\[ \begin{aligned} Q_C &= \omega C V^2 \\ C &= \frac{Q_C}{\omega V^2} = \frac{Q_C}{2\pi f V^2} \end{aligned} \]周波数fを50Hzとすると:
\[ \begin{aligned} C &= \frac{926}{2\pi \times 50 \times 100^2} \\ &= \frac{926}{3.14 \times 10^6} \\ &\approx 295 \times 10^{-6} \\ &= 295 \ \mathrm{[\mu F]} \end{aligned} \]したがって、力率を0.58から0.9に改善するには、約295μFのコンデンサを並列に接続する必要があります。
素晴らしい計算や!力率改善のためのコンデンサ容量の計算をバッチリできてるな。
ちょっと違う視点から考えてみよか。三相交流のバランスのとれた回路で、線間電圧が200V、線電流が10A、力率が0.8の負荷があるとする。この負荷の有効電力と無効電力はいくらになるやろか?
はい、先生!三相交流のバランスのとれた回路の計算をします。
三相交流の電力計算では、以下の公式を使います:
\[ \begin{aligned} P &= \sqrt{3} \times V_L \times I_L \times \cos \phi \\ Q &= \sqrt{3} \times V_L \times I_L \times \sin \phi \\ S &= \sqrt{3} \times V_L \times I_L \end{aligned} \]ここで:
- P:有効電力 [W]
- Q:無効電力 [var]
- S:皮相電力 [VA]
- VL:線間電圧 [V]
- IL:線電流 [A]
- cos φ:力率
与えられた条件:
- 線間電圧 VL = 200 V
- 線電流 IL = 10 A
- 力率 cos φ = 0.8
有効電力Pを計算します:
\[ \begin{aligned} P &= \sqrt{3} \times V_L \times I_L \times \cos \phi \\ &= \sqrt{3} \times 200 \times 10 \times 0.8 \\ &= 1.732 \times 200 \times 10 \times 0.8 \\ &= 2771.2 \ \mathrm{[W]} \\ &\approx 2.77 \ \mathrm{[kW]} \end{aligned} \]無効電力Qを計算します:
\[ \begin{aligned} \sin \phi &= \sin(\cos^{-1}(0.8)) \\ &= \sin(36.87^{\circ}) \\ &= 0.6 \\ Q &= \sqrt{3} \times V_L \times I_L \times \sin \phi \\ &= \sqrt{3} \times 200 \times 10 \times 0.6 \\ &= 1.732 \times 200 \times 10 \times 0.6 \\ &= 2078.4 \ \mathrm{[var]} \\ &\approx 2.08 \ \mathrm{[kvar]} \end{aligned} \]したがって、この三相負荷の有効電力は約2.77 kW、無効電力は約2.08 kvarです。
ほんまによう計算できてるな!三相交流の電力計算も完璧や!
さあ、最後にまとめをしよか。力率についての重要なポイントを整理してみよ。
- 力率とは何か?なぜ重要か?
- 力率の改善方法は?
- 力率改善のメリットは?
これらについて簡単にまとめてくれるか?
はい、先生!力率についての重要なポイントをまとめます。
1. 力率とは何か?なぜ重要か?
力率(パワーファクター)とは、皮相電力に対する有効電力の比率で、cos φ で表されます。電圧と電流の位相差を示し、0から1の値をとります。
力率が重要な理由:
- 電力の効率的な利用に直結します(高い力率=効率的な電力利用)
- 低い力率は送電設備の容量を圧迫し、損失を増加させます
- 多くの電力会社は低い力率に対してペナルティ料金を設定しています
- 電気設備の容量決定に影響します
2. 力率の改善方法は?
力率の改善方法:
- 誘導性負荷(モーター、変圧器など)には並列にコンデンサを接続
- 容量性負荷(まれですが)には直列にリアクトルを接続
- 同期調相機の利用(大規模設備の場合)
- 電力用能動フィルタの使用(高調波対策も兼ねる)
- 負荷設備自体の見直し(高力率機器への更新)
3. 力率改善のメリットは?
力率改善のメリット:
- 電力料金の削減(多くの場合、力率割引が適用される)
- 送電線・配電線の損失減少
- 電気設備容量の有効活用(同じ設備でより多くの有効電力を得られる)
- 電圧変動の抑制と安定化
- 電気設備の寿命延長
- 系統全体の効率向上(社会的メリット)
力率の管理は、電気主任技術者として非常に重要な業務の一つです。適切な力率管理により、設備の効率向上とコスト削減を両立させることができます。
めっちゃええまとめやな!力率の概念、計算方法、改善方法、そしてそのメリットまでしっかり理解できてるやん。
第三種電気主任技術者試験では、こういった力率の計算や改善方法についての問題がよく出るから、今日学んだことはしっかり覚えておくんやで。
特に:
- 力率の計算式: cos φ = R/Z = R/√(R²+X²)
- 三相電力の計算式: P = √3・VL・IL・cos φ
- 力率改善に必要なコンデンサ容量の計算
これらは試験でも重要やし、実務でもめっちゃ使うから、しっかり覚えてな!他に質問あるか?
ありがとうございます、先生!力率についてとても分かりやすく教えていただきました。一つ質問があります。
実際の現場では、力率計測はどのような機器や方法で行うのでしょうか?また、力率改善用のコンデンサはどのように選定し、設置するのが一般的なのでしょうか?
ええ質問やな!実務的な観点からも考えてるのはエライで!
まず、力率の計測方法やけど、大きく分けて3つあるんや:
- 力率計による直接測定:力率計っていう専用の計器があって、これは電圧と電流の位相差を直接測定するんや。単相用と三相用があるけど、これを回路に接続して直読するのが一番シンプルな方法やな。
- 電力計と電流計・電圧計による測定:有効電力P(ワットメーターで測定)と皮相電力S(電圧計と電流計の積)を別々に測って、P÷Sで力率を計算する方法もよく使われるで。
- デジタルパワーアナライザー:最近はこれが主流やな。これは電圧・電流・電力・力率などを同時に測定できる高機能な測定器や。高調波成分の分析もできたりして、力率だけでなく電力品質全体を評価できるんや。
次に、力率改善用コンデンサの選定と設置やけど:
- 容量選定:まず現在の力率を測定して、目標力率(通常は0.95〜0.98)との差から必要な無効電力を計算するんや。これは今日やったような計算式を使うんやけど、設備の運用状況(負荷変動)も考慮せなあかんで。
- 設置方法:大きく分けて集中補償と個別補償があるんや。
- 集中補償:受電点の近くに大容量のコンデンサバンクを設置する方法
- 個別補償:各モーターなど力率の悪い機器ごとに小容量のコンデンサを設置する方法
- 自動力率調整装置:負荷が変動する場合は、力率を自動的に検出して適切なコンデンサ容量を接続・遮断する装置(APFC:Automatic Power Factor Controller)を使うんや。これはコンデンサを複数段に分けて、必要な分だけ接続するシステムや。
実務ではこういった知識も大事やから、覚えておくといいで!
ありがとうございます、先生!実務的な知識も教えていただき、とても参考になりました。力率計測機器の種類や、力率改善用コンデンサの選定・設置方法についてよく理解できました。
特に、集中補償と個別補償の違いや、負荷変動がある場合の自動力率調整装置の必要性は、実際の現場で役立ちそうですね。電気主任技術者として働く際には、こういった実務的な知識も重要だと思います。今日は貴重な知識をありがとうございました!
おお、ええ反応やな!実務的な視点を持つのは電気主任技術者として大事なことやで。
今日は力率について勉強したけど、これは電気設備の効率にも直結する大事なテーマやから、しっかり覚えておいてな。試験対策としても、実務知識としても、両方で役立つで!
また何か質問があれば、いつでも聞いてな!次回もがんばろう!
ありがとうございます、先生!とても分かりやすい授業でした。力率の概念から計算方法、実務での応用まで幅広く学べて、非常に有意義でした。次回もよろしくお願いします!
解説まとめ
「有効電力 𝐏 [W] と無効電力 𝐐 [var]」の通り,回路の力率 \( \cos \phi \) は次のように求められます:
\( \cos \phi = \frac{R}{\sqrt{R^2 + X_{\mathrm{L}}^2}} \)
\( = \frac{R}{\sqrt{R^2 + \left( \sqrt{2}R \right)^2}} \)
\( = \frac{R}{\sqrt{R^2 + 2R^2}} \)
\( = \frac{R}{\sqrt{3R^2}} \)
\( = \frac{R}{\sqrt{3}R} \)
\( = \frac{1}{\sqrt{3}} \)
\( \approx 0.58 \)
したがって,この回路の力率は約 0.58 となります。